Lecture 05 - Kinematics 3

---

Properties of Rotation Transform Matrices Angular Velocities Angular Acceleration

Gyroscope Example

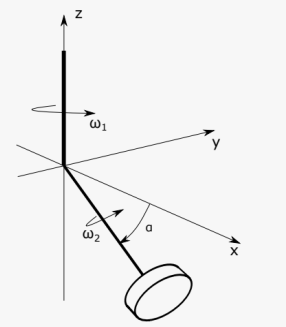
Gyroscope Example 2

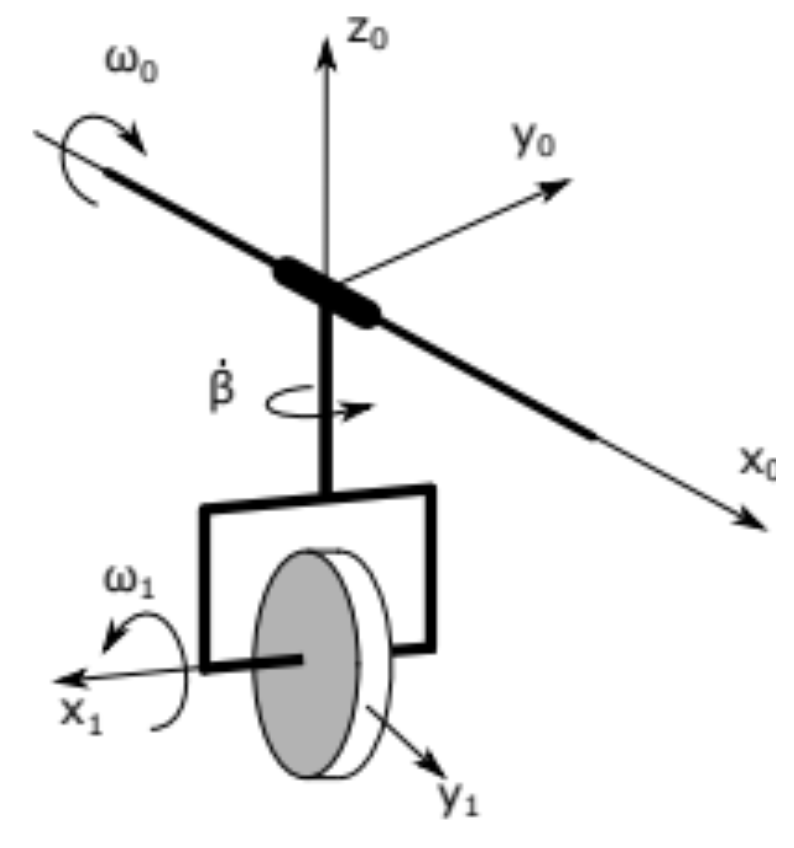Goal: Find the acceleration, ${\vec{\alpha }}_0$.

How to solve: We find ${\vec{\Omega }}_0$ and ${\vec{\Omega }}_1$

$$\begin{array}{rl}{\vec{\Omega }}_0& =-{\omega }_0{\vec{i}}_0\\ {\vec{\Omega }}_1& =-{\omega }_0{\vec{i}}_0+\dot{\beta }{\vec{k}}_0\end{array}$$

We then find the acceleration, ${\vec{\alpha }}_0$.

$${\vec{\alpha }}_0=-{\dot{\vec{\omega }}}_0{\vec{i}}_0+\ddot{\beta }{\vec{k}}_0+{\dot{\omega }}_1{\vec{i}}_1+{\omega }_0({\vec{\Omega }}_0\times -{\vec{i}}_0)+\dot{\beta }({\vec{\Omega }}_1\times {\vec{k}}_1)+{\omega }_1({\vec{\Omega }}_1\times {\vec{i}}_1)$$

Where

$$\begin{array}{rl}{\vec{i}}_0& =\cos (\beta ){\vec{i}}_1-\sin (\beta ){\vec{i}}_1\\ {\vec{i}}_1& =\end{array}$$

Giving us the expression for ${\vec{\alpha }}_1$

$${\vec{\alpha }}_0=\dot{\beta }{\omega }_0\sin (\beta ){\vec{i}}_1+({\omega }_1\dot{\beta }+\dot{\beta }{\omega }_0\cos \beta ){\vec{i}}_1+(\ddot{\beta })$$